Kvant. Дивовижна пляшка - PhysBook

Ромішевський Е. Дивовижна пляшка // Квант. - 2001. - № 1. - С. 27-29.

За спеціальною домовленістю з редколегією та редакцією журналу "Квант"

Багато загадкових фізичних явищ пов'язано зі звичайною скляною пляшкою і міститься в ній рідиною. Наприклад, можна запитати себе чи друзів: як швидше наповнити або спорожнити пляшку; як цікавіше її втопити або витягти з неї щільну пробку? Зараз ми розглянемо дещо незвичну проблему: як розбити таку пляшку з рідиною голими руками (не використовуючи будь-яких інших фізичних тіл), при цьому, природно, не поранивши руки?

Уявімо такий експеримент. Візьмемо для конкретності звичайну півлітрову пляшку, що має форму двох циліндрів - основної частини і горлечка. Маса порожньої пляшки приблизно дорівнює m b = 0,5 кг. Наллємо в неї води стільки, щоб майже повністю заповнити основну циліндричну частину. При цьому маса води буде такою ж, як і пляшки: m v = 0,5 кг. Однією рукою візьмемо пляшку за шийку і помістимо її над порожнім відкритим відром. Потім, розмахнувшись, різко вдаримо по шийки м'якою подушкою долоні ... Дно пляшки і її нижня частина разом з водою опиняться у відрі, а верхня частина пляшки з охоплених шийкою - в сухий руці. Вельми ефектне видовище!

Тепер спробуємо все це осмислити і зробити кількісні оцінки.

Головним результатом досвіду є розбите скло, що має досить велику товщину (порядку декількох міліметрів). Щоб розбити таке скло, потрібно створити досить великі сили. Звідки вони беруться?

Уявімо собі письмовий стіл, покритий товстим прозорим склом. Нехай на склі лежить сталевий пружний кулька масою 100 г. На кульку діють дві сили: сила тяжіння \ (~ m \ vec g \), прикладена в центрі кульки, і сила реакції поверхні столу \ (~ \ vec F_r \), що дорівнює силі тяжіння за величиною, але протилежно спрямована і прикладена в місці торкання поверхонь кульки і столу. Безпосередньо до поверхні скла в тому ж місці торкання прикладена сила тиску \ (~ \ vec F_d \) з боку кульки, рівна (відповідно до третього закону Ньютона) за величиною силі реакції, але протилежна їй за напрямком. Таким чином, в місці торкання на скло діє сила тиску

\ (~ F_d = F_r = mg \) = 1 Н.

Цією сили явно недостатньо, щоб зруйнувати скло на столі. Однак, якщо кулька підняти над поверхнею столу сантиметрів на двадцять і відпустити, то він, ударившись, безсумнівно розіб'є скло.

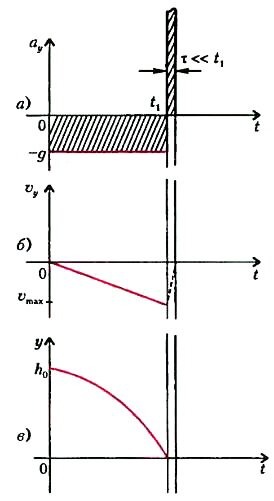
Мал. 1

Розглянемо процес докладніше. Направимо вісь Y вгору над поверхнею скла і зобразимо графічно залежності прискорення, швидкості і висоти кульки від часу (рис.1). Особливо виділимо відрізок часу удару τ, протягом якого кулька взаємодіє зі склом. Як відомо, при вільному падінні прискорення кульки a y = - g, швидкість υ y = - gt і висота \ (~ y = h_0 - \ frac {gt ^ 2} {2} \). Для розглянутого випадку h 0 = 20 см, час падіння \ (~ t_1 = \ sqrt {\ frac {2h_0} {g}} \) = 0,2 с, максимальна швидкість \ (~ \ upsilon_ {max} = gt_1 = \ sqrt {2gh_0} \) = 2 м / с.

Оцінимо час τ зіткнення кульки з поверхнею скла. Руйнування скла настає при деякій величині деформації його поверхні в місці контакту. На підставі досвідчених даних можна прийняти в якості такої величини δ = 0,1 мм = 10-4 м. Значення швидкості за час удару змінюється від υ max до нуля, звідки час удару \ (~ \ tau = \ frac {\ delta} { \ frac {\ upsilon_ {max}} {2}} \) = 10-4 с (тут вважається, що швидкість лінійно падає з часом). Ми отримали, що τ приблизно в тисячу разів менше часу падіння t 1. Легко зрозуміти, що два заштрихованих прямокутника на малюнку 1, а мають одну і ту ж площу, рівну

\ (~ \ Upsilon_ {max} = gt_1 = \ sqrt {2gh_0} \).

Зміна швидкості протягом часу τ (ми маємо на увазі абсолютно непружних удар, тому що скло зруйнується ще при його стисканні) теж одно υ max, а значить, пов'язане з цим середнє прискорення (уповільнення) \ (~ \ bar a = \ frac { \ upsilon_ {max}} {\ tau} = 10 ^ 3 g \) виявиться приблизно в тисячу разів більше д - ось це «перевантаження»! Таким чином, на графіку прискорення висота позитивного піку, що відповідає величині \ (~ \ bar a \), буде в тисячу разів вище g.

Тепер оцінимо силу удару кульки по склу. Вона теж буде в тисячу разів більше сили тяжіння:

\ (~ F_ {ud} = m \ bar a = \ frac {mg t_1} {\ tau} \) ≈ 103 Н.

Це вже цілком відчутна величина.

Сили, що діють під час удару, називають «миттєвими» силами. В процесі удару, що триває дуже короткий час τ, вони різко збільшуються від нуля до деякого максимуму, а потім знову падають до нуля. Під силами удару можна розуміти середнє значення миттєвих сил за короткий час удару, так щоб вираз \ (~ F_ {ud} \ tau = m \ Delta \ upsilon \) представляло собою зміну імпульсу тіла за цей час (величину \ (~ F_ {ud } \ tau \) називають імпульсом сили).

Вже давно було відомо: щоб отримати «виграш, - в силі, можна використовувати важіль. Потрібно вибрати його точку опори так, щоб мала сила F m мала велике плече l b, а «виграшна» велика сила F b - мале плече l m. При цьому \ (~ F_b = F_m \ frac {l_b} {l_m} \). У цьому сенсі удар є своєрідним важелем - тимчасовим важелем. Мала сила протягом великого часу t 1, розганяє кульку, а величезна сила удару F ud за малий час τ зупиняє його, причому \ (~ F_ {ud} = mg \ frac {t_1} {\ tau} \ approx mg \ cdot 10 ^ 3 \). Можна образно сказати, що в нашому випадку отриманий «виграш» в силі в тисячу разів.

Відзначимо ще одну важливу властивість удару. При зіткненні дуже твердих тіл, для яких деформації можна вважати нескінченно малими: δ → 0, швидкості змінюються на кінцеві величини: Δ υ ~ υ. Оцінка часу удару \ (~ \ tau \ approx \ frac {\ delta} {\ upsilon} \) теж дасть нескінченно малу величину: τ → 0. З другого закону Ньютона, записаного у вигляді \ (~ m \ Delta \ upsilon = F_ {ud} \ tau \), видно, що твір \ (~ F_ {ud} \ tau \) є величиною кінцевої. Значить, \ (~ F_ {ud} \ to \ infty \), тобто величина ударної сили велика, і в порівнянні з нею можна нехтувати всіма іншими кінцевими силами, що діють під час удару (наприклад, силою тяжіння).

Отже, тепер саме час повернутися до експерименту з пляшкою.

Для того щоб скло пляшки лопнуло у її дна, необхідно з цього дну добре вдарити. Але чим? Рукою? Ні, тому що рукою зробити удар такої сили неможливо. До того ж, ми вдарили рукою за шийку - здавалося б, повинно розбитися шийку. Залишається припустити, що цей удар по дну її вода, що міститься в пляшці. Але для цього потрібно спочатку воду «підняти» від скляного дна на деяку висоту і потім надати їй можливість «впасти» на нього. Адже вода нестислива, і її зіткнення з пляшкою нагадує удар важкого пружного кульки об скло. Виходить, що потрібно вдарити по шийки з такою силою, щоб прискорення пляшки було більше прискорення маси води - тільки тоді між водою і дном пляшки зможе утворитися порожній обсяг, в якому тиск буде близьке до нуля. Потім після удару по шийки, який триває мале час, відбувається потужне «схлопування» води і пляшки під дією атмосферного тиску. Зіткнення між водою і пляшкою, відбувається за дуже малий час і, як ми вже відзначали, призводить до дуже великим руйнівним силам і тисків.

Проведемо необхідні кількісні оцінки. Перш за все поставимо головне питання: яка мінімальна величина сили удару по шийки, достатня для того, щоб відірвати воду від дна пляшки? Для цього розглянемо основні діючі сили. На воду зверху діє сила атмосферного тиску \ (~ F ^ v_a = p_a S \), де S - перетин основний циліндричної частини пляшки. Будемо вважати, що p a = 105 Па, а S = πr 2 = 30 см2 (це відповідає значенню радіуса r ≈ 3,1 см); тоді F va = 300 Н. Під дією цієї сили вся маса води m = 0,5 кг придбає прискорення

\ (~ a_v = \ frac {F ^ v_a} {m} \) = 600 м / с2 = 60 g.

На пляшку діють наступні сили: зверху на горлечко діє сила нашого удару F, а знизу на дно пляшки діє сила атмосферного тиску \ (~ F ^ b_a = p_a S \) = 300 Н. Для того щоб пляшка придбала прискорення більше, ніж вода ( маса пляшки приблизно дорівнює масі води), потрібно, щоб виконувалася нерівність

\ (~ F - F ^ b_a> F ^ v_a \).

тобто сила нашого удару повинна бути більше подвоєною сили атмосферного тиску:

\ (~ F> F ^ b_a + F ^ v_a = 2F_a \) = 600 Н.

Розглянемо тепер докладніше першу фазу процесу - удар по шийки. Припустимо, що ми трохи перевищили величину мінімальної необхідної сили і вдарили з силою F 1 = 650 Н. Тоді пляшка матиме прискорення

\ (~ a_ {b1} = \ frac {F_1 - F_a} {m} \) = 700 м / с2 = 70 g,

а вода отримає прискорення

\ (~ a_ {v1} = \ frac {F_a} {m} \) = 60 g.

Будемо вважати, що час удару порядку сотої частки секунди, тобто τ 1 = 10-2 с, і оцінимо товщину вакуумного шару Δ h, тобто відстань, на яке розійдуться пляшка і вода:

\ (~ \ Delta h = \ frac {\ Delta a \ tau ^ 2_1} {2} = \ frac {10g \ tau ^ 2_1} {2} \) = 5 · 10-3 м = 5 мм.

При цьому вода і пляшка придбають такі швидкості:

\ (~ \ Upsilon_ {v1} = 60g \ tau_1 \) = 6 м / с, \ (~ \ upsilon_ {b1} = 70g \ tau_1 \) = 7 м / с.

Після припинення дії зовнішньої сили (тобто після закінчення часу τ 1) починається друга фаза процесу. Тепер на пляшку буде діяти тільки сила атмосферного тиску, спрямована вгору, яка повідомить пляшці прискорення

\ (~ a_ {b2} = - \ frac {p_a S} {m} \) = -60 g.

Це прискорення буде сповільнювати рух пляшки:

\ (~ \ Upsilon_ {b2} = \ upsilon_ {b1} - | a_ {b2} | t \),

вода ж буде продовжувати рух з прискоренням

\ (~ A_ {v2} = a_ {v1} = +60 '' g '' \),

і швидкістю

\ (~ \ Upsilon_ {v2} = \ upsilon_ {v1} + a_ {v2} t \).

Зіткнення між водою і пляшкою відбудеться ще через час τ 2, за яке відстань між ними скоротиться від Δ h до нуля:

\ (~ \ Tau_2 = \ frac {\ upsilon_ {b1} - \ upsilon_ {v1}} {2a_v} + \ sqrt {\ frac {(\ upsilon_ {b1} - \ upsilon_ {v1}) ^ 2} {(2a_v ) ^ 2} + \ frac {\ Delta h} {a_v}} \).

Оцінку для цього часу отримаємо зі співвідношення

\ (~ \ Delta h = \ frac {\ Delta a \ tau ^ 2_2} {2} \),

де Δ a = a v2 - a b2 = 2 a v = 120g:

\ (~ \ Tau_2 = \ sqrt {\ frac {2 \ Delta h} {2a_v}} \) = 3 · 10-3 с.

Потім оцінимо значення швидкостей води і пляшки безпосередньо перед їх зіткненням:

\ (~ \ Upsilon_ {v2} = \ upsilon_ {v1} + a_ {v2} \ tau_2 \) = 7,8 м / с, \ (~ \ upsilon_ {b2} = \ upsilon_ {b1} - | a_ {b2 } | \ tau_2 \) = 5,2 м / с.

Виходить, що вода доганяє пляшку і, б'ючи, може розбити її.

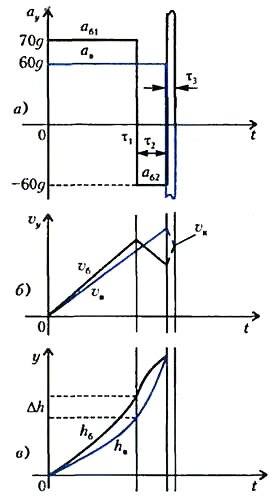
Мал. 2

Оцінимо тепер, які сили і тиску будуть виникати безпосередньо при зіткненні - це вже третя фаза процесу. Будемо вважати удар абсолютно непружним (руйнування скла) і його характерний час рівним τ 3 = 10-4 с (як для кульки на склі). Тоді зміна імпульсу кожного тіла дорівнюватиме

\ (~ M \ Delta \ upsilon = m \ left (\ upsilon_ {v2} - \ frac {\ upsilon_ {v2} + \ upsilon_ {b2}} {2} \ right) = m \ left (\ frac {\ upsilon_ {v2} - \ upsilon_ {b2}} {2} \ right) \) = 0,65 кг · м / с,

а сила удару

\ (~ F_ {ud} = \ frac {m \ Delta \ upsilon} {\ tau_3} \) = 6,5 · 103 Н.

Тиск у дна пляшки при цьому складе

\ (~ P = \ frac {F_ {ud}} {S} = \ frac {6,5 \ cdot 10 ^ 3} {30 \ cdot 10 ^ {- 4}} \) ≈ 22 атм

- досить вражаюча величина! Оскільки товщина скла бічній поверхні пляшки зазвичай менше, ніж товщина дна (а «де тонко, там і рветься»), руйнування скла відбувається саме на бічній поверхні пляшки поблизу її дна.

Подібно малюнку 1, на малюнку 2 представлений графічно весь процес протягом сумарного часу τ 1 + τ 2 + τ 3, яке має порядок сотої частки секунди. На всю систему (пляшку з водою загальною масою m = m v + m b = 1 кг) подіяв імпульс ударної сили

\ (~ F_1 \ tau_1 \) = 650 Н · 10-2 с = 6,5 Н · с.

В результаті після закінчення процесу, тобто після непружного удару зі швидкістю

\ (~ \ Upsilon_k = \ frac {\ upsilon_ {v2} + \ upsilon_ {b2}} {2} \) = 6,5 м / с,

отриманий імпульс

\ (~ M \ upsilon_k \) = 1 кг · 6,5 м / с = 6,5 кг · м / с,

Видно, що має місце рівність

\ (~ F_1 \ tau_1 = m \ upsilon_k \).

Чи випадково це? Звичайно, ні! Адже сили атмосферного тиску діють тут окремо на воду і на пляшку, а в загальній системі пляшки з водою вони знищують один одного, і залишається тільки зовнішня сила.